空间解析几何与向量代数
例一
例题一.求过点 P(1,−1,0)且与两向量a=(−2,−2,1),b=(−1,0,2)平行的平面方程
①根据a,b求出对应的平面法向量
n(i,j,k)=a×b得到n(−4,3,−2)
②将法向量分量代入一般方程
Ax+By+Cz+D=0得到−4x+3y+−2z+D=0
把P点代入得到D=7
∴ 平面方程是−4x+3y−2z+7=0
知识点总结:
向量叉乘
向量的叉乘(Cross Product),也称为向量积,是三维空间中两个向量的一种特殊乘法运算。它产生第三个与前两个向量都垂直的向量,并且结果向量的长度和方向与原向量构成平行四边形的面积有关。以下是向量叉乘的主要性质和计算方法:
定义
设有两个向量 A 和 B,它们的叉乘表示为 A × B,结果是一个向量。
计算方法
设向量 A = (a1, a2, a3) 和向量 B = (b1, b2, b3),它们的叉乘计算如下:
A×B=∣∣ia1b1ja2b2ka3b3∣∣
其中,i, j, k 分别是沿 x、y、z 轴的单位向量。根据行列式的定义,计算结果为:
A×B=(a2b3−a3b2)i−(a1b3−a3b1)j+(a1b2−a2b1)k
平面方程
一般式:Ax+By+Cz+D=0
截距式:ax+by+cz=1
点法式:(x−x0)A+(y−y0)B+(z−z0)C=0
例二
例题二.设向量a=2i−4j+k,b=i−j−3k,则a⋅b=3.
知识点:
a · b = (a1∗b1)+(a2∗b2)+(a3∗b3)=(2∗1)+(−4∗−1)+(1∗−3)=3
例三
例题三.球面x2+y2+z2=14在点(1,2,3)处的法线方程为

总结:
①求偏导把点带进去
②用对称式方程得出结果
例题四
例题四.求解一条直线的方程,该直线通过点 (0,2,4) 并且与两个平面 x+2z=1 和 y-3z=2 平行。

例题五



函数与积分
例题一.极大极小值








曲线积分
拉格朗日乘数法
第一题
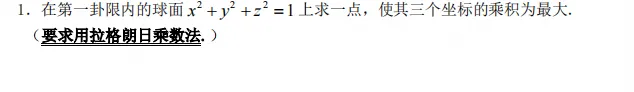

第二题